Pewarnaan graf adalah kasus khusus dari pelabelan graf. Pelabelan
disini maksudnya, yaitu memberikan warna pada titik-titik pada batas
tertentu.
Ada tiga macam pewarnaan graf.
Pertama, pewarnaan titik (vertex coloring) yaitu memeberikan warna berbeda pada setiap titik yang bertetangga sehingga tidak ada dua titik yang bertengga dengan warna yang sama.

Kedua, pewarnna sisi (edge coloring), yaitu memberikan warna berbeda pada sisi yang bertetangga sehingga tidak ada dua sisi yang bertetangga memepunya warna yang sama.

Ketiga, pewarnaan bidang, yaitu memberikan warna pada bidang sehingga tidak ada bidang yang bertetangga mempunyai warna yang sama.

Ada tiga macam pewarnaan graf.
Pertama, pewarnaan titik (vertex coloring) yaitu memeberikan warna berbeda pada setiap titik yang bertetangga sehingga tidak ada dua titik yang bertengga dengan warna yang sama.

Kedua, pewarnna sisi (edge coloring), yaitu memberikan warna berbeda pada sisi yang bertetangga sehingga tidak ada dua sisi yang bertetangga memepunya warna yang sama.

Ketiga, pewarnaan bidang, yaitu memberikan warna pada bidang sehingga tidak ada bidang yang bertetangga mempunyai warna yang sama.

| DEFINISI 1 |
| Pewarnaan simpul (Vertex coloring), singkatnya pewarnaan (coloring),suatu Graf adalah pemberian warna terhadap simpul sedemikian sehingga dua simpul yang berdampingan mempunyai warna yang berlainan. |
| DEFiNISI 2 |
| Kita katakan G berwarna n,bila terdapat pewarnaan dengan menggunakan n warna. |
| DEFINISI 3 |
| Jumlah minimum warna yang dibutuhkan disebut bilangan khromatis dari G,ditulis K(G). |
| Dalam memecahkan problem pewarnaan ,kita selalu berusaha mewarnai simpul menggunakan banyak warna minimal. |
| ALGORITMA WELCH-POWELL |
| Kita dapat menggunakan algoritma Welch-Powell untuk mewarnai suatu Graf, an banyak warna minimal, sebagai berikut; |
| Mula-mula kita urutkan semua simpul berdasarkan derajatnya, dari derajat besar ke derajat kecil. Ambil warna pertama, warnai simpul pertama (dalam urutan), kemudian simpul berikutnya yang tidak berdampingan, terus menerus, berdasarkan urutan. Kemudian kita lanjutkan dengan warna kedua dan seterusnya, sampai semua simpul telah diberi warna. |
| Contoh : |
| Kita akan mewarnai simpul Graf menggunakan algoritma Welch-powell. |
 |
| Urutan simpul berdasarkan deraiatnya: |
| E. G, C, A, B, D, F, H |
| Ambil warna pertama. misalnya hijau. Beri wama hijau simpul E, kemudian warnai simpul A, karena A tidak berdampingan dengan simpul E. |
| Urutan simpul yang belum diberi warna: |
| G, C, B, D, F, H |
| Ambil warna kedua, misalnya merah, beri warna merah simpul G,B dan F. |
| Urutan simpul yang belum diberi warna |
| C, D. H |
| Warna ketiga, misalnya putih, beri warna putih simpul C, D dan H. |
| Pewarnaan telah selesai, Graf merupakan. Graf berwarna 3. |
| Dapat dicatat bahwa Graf bukan Graf berwarna 2, karena misalnya simpul A, B dan D harus mempunyai warna yang berbeda. Jadi K(G) = 3. |
| Berikut ini teorema mengenai Pewarnaan Graf |
| Teorema 1 |
| Pernyataan berikut adalah ekivalen : |
| (I) G berwarna 2 |
| (2) G adalah bipartisi |
| (3) Setiap Sirkuit dalam G mempunyai panjang genap |
| Dengan mudah dilihat bahwa Graf lengkap dengan n simpul Kn membutuhkan n warna dalam setiap pewarnaan, karena masing-masing simpul berdampingan dengan simpul yang lain. |
| Berikut ini teorema bagi Graf Planar |
| Teorema 1 |
| Suatu Graf Planar G adalah berwarna 5 |
| PEWARNAAN MAP |
| Perhatikan suatu Map M. Dua Region dari M dikatakan berdampingan jika mereka mempunyai suatu ruas persekutuan .Sebagai contoh pada Gambar. Region R2 dan R3 adalah berdampingan, sedangkan Region R3 dan R5 tidak berdampingan. |
| DEFINISI |
| Yang dimaksud dengan pewarnaan Map adalah pemberian warna Region sedimikian sehingga Region yang berdampingan mempunyai warna yang berbeda. |
| Suatu Map M berwarna n jika terdapat suatu pewarnaan dari M dengan menggunakan n warna. Graf pada Gambar adalah berwarna 3, karena Region dapat diberi warna sebagai berikut |
| R1 merah, R2 putih, R3 merah, R4 putih, R5 merah, R6 biru |
| Di sini 3 adalah banyak warna minimal |
 |
| Andaikata kita menggambar sebuah simpul baru pada masing-masing Region suatu Map M, kemudian membuat sebuah ruas menghubungkan simpul pada 2 Region yang berdampingan memotong setiap ruas batas/persekutuan kedua Re¬gion, dengan tanpa adanya ruas baru yang berpotongan, maka akan terbentuk suatu Map M* yang disebut Dual dari Map M. |
| Perhatikan dual dari Map Gambar 1.35: |
| Dapat dilihat bahwa masing-masing Region dar M* mengandung tepat satu simpul dari M demikian pula setiap ruas dari M memotong tepat satu ruas dari M* karena itu dapat dikatakan juga bahwa M adalah dual dari M*. Relasi Dual adalah relasi yang simetris. |
| Dapat diamati bahwa pewarnaan region dari M sama artinya dengan pewarnaan simpul dari M*. Dengan perkataan lain: |
| Suatu map M berwarna n jika dan hanya jika dualnya M* berwarna (simpul) n. |
| Jadi diperoleh teorema |
| Teorema 1: |
| Suatu map M adalah berwarna 5 |
| Namun tidak ada map yang dijumpai membutuhkan 5 warna pada setiap pewarnaan. |
| Teorema 2: |
| Setiap map adalah berwarna (region) 4, dan setiap Graf planar adalah berwarna (simpul)4. |
| Teorema ini dibuktikan oleh Apple dan Haken pada tahun 1976 dengan menggunakan computer untuk menganalisis sampai 2000 Graf yang mengandung jutaan kasus. |





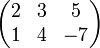 Matriks di atas berordo 2x3.
Matriks di atas berordo 2x3. maka matriks transposenya (At) adalah
maka matriks transposenya (At) adalah

 maka
maka 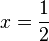
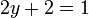 maka
maka 
 maka
maka 



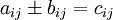

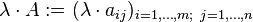



 ) adalah:
) adalah:
 maka tentukan
maka tentukan 
 maka tentukan
maka tentukan 
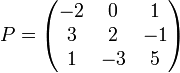
 dengan ekspansi baris pertama!
dengan ekspansi baris pertama!
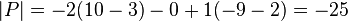
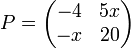


 vs
vs